MATHS :: Lecture 07 :: Differential Equations
![]()
Differential Equations
Differential equation is an equation in which differential coefficients occur.
A differential equation is of two types
(1) Ordinary differential equation
(2) Partial differential equation
An ordinary differential equation is one which contains a single independent variable.
Example:
![]()
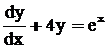
A partial differential equation is one containing more than one independent variable.
Examples
Here we deal with only ordinary differential equations.
Definitions
Order
The order of a differential equation is the order of the highest order derivative appearing in it.
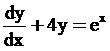 Order 1
Order 1
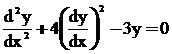 Order -2
Order -2
Degree
The degree of a differential equation is defined as the degree of highest ordered derivative occurring in it after removing the radical sign.
First-order linear ODEs3-Laplace transform
First-order linear ODEs2- constant coefficients
Give the degree and order of the following differential equation.
1) 5 (x+y)
2)
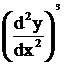 - 6
- 63)
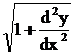 = 3
= 3Squaring on both sides
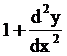 = 9
= 9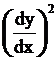 +6
+6degree -1, order 2
4)
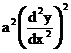
1+3
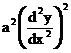
degree – 2, order – 2
Note
If the degree of the differential equations is one. It is called a linear differential equation.
Formation of differential equations
Given the solution of differential equation, we can form the corresponding differential equation. Suppose the solution contains one arbitrary constant then differentiate the solution once with respect to x and eliminating the arbitrary constant from the two equations. We get the required equation. Suppose the solution contains two arbitrary constant then differentiate the solution twice with respect to x and eliminating the arbitrary constant between the three equations.
Solution of differential equations
- Variable separable method,
- Homogenous differential equation
iii) Linear differential equation
Variable separable method
Consider a differential equation ![]() = f(x)
= f(x)
Here we separate the variables in such a way that we take the terms containing variable x on one side and the terms containing variable y on the other side. Integrating we get the solution.
Note
The following formulae are useful in solving the differential equations
- d(xy) = xdy +ydx
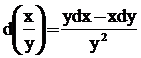
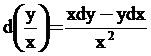
Homogenous differential equation
![]() Consider a differential equation of the form
Consider a differential equation of the form
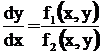 (i)
(i)
where f1 and f2 are homogeneous functions of same degree in x and y.
![]()
Here put y = vx
Substitute equation(ii) in equation (i) it reduces to a differential equation in the variables v and x. Separating the variables and integrating we can find the solution.
Linear differential equation
A linear differential equation of the first order is of the form
To solve this equation first we find the integrating factor given by
Integrating factor = I.F =
Then the solution is given by
| Download this lecture as PDF here |
![]()